Views
Document
Event
File
Folder
Image
Link
News Item
Photo
Photo Album
Topic
Weblog
Wiki Page
グラフ構造
Document Actions
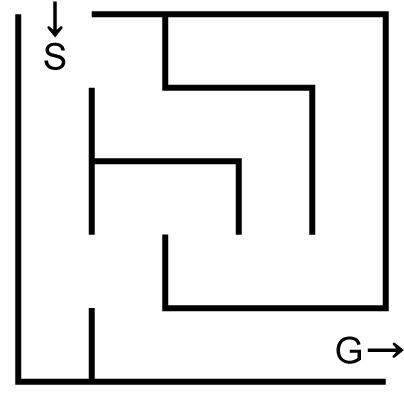
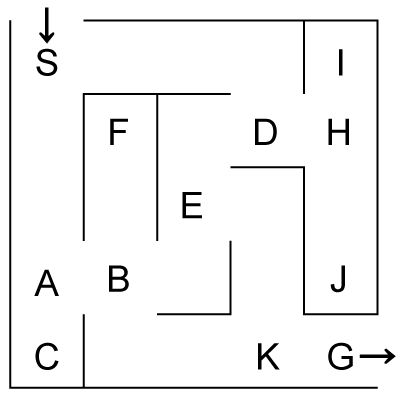
たとえば迷路
分岐点・終端点
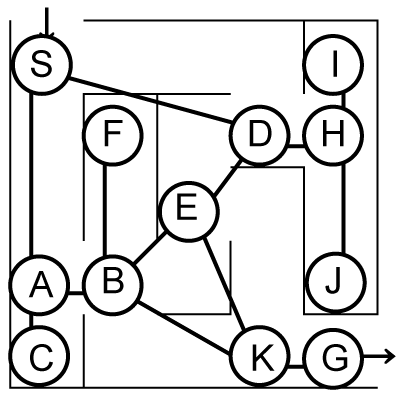
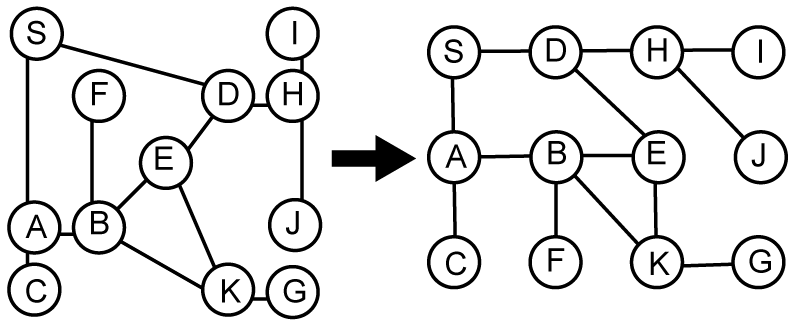
グラフ
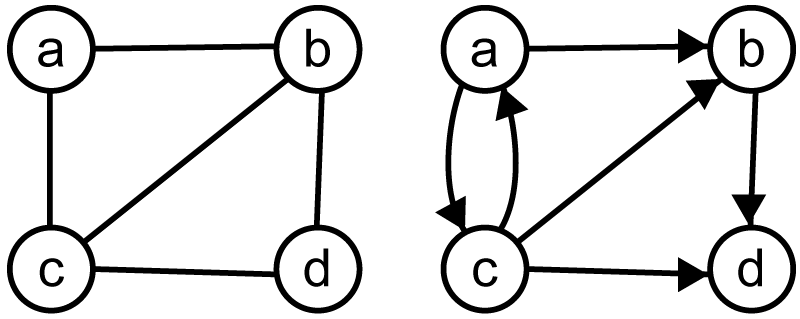
無向グラフと有向グラフ
グラフを表すデータ構造
- 順配置表現
- リンク配置表現
隣接行列（無向グラフ）
A1 = [[0, 1, 1, 0], # a [1, 0, 1, 1], # b [1, 1, 0, 1], # c [0, 1, 1, 0]] # d
隣接行列（有向グラフ）
A2 = [[0, 1, 1, 0], # a -> x [0, 0, 0, 1], # b -> x [1, 1, 0, 1], # c -> x [0, 0, 0, 0]] # d -> x
接続行列（無向グラフ）
B1 = [[1, 1, 0, 0, 0], # a [1, 0, 1, 1, 0], # b [0, 1, 1, 0, 1], # c [0, 0, 0, 1, 1]] # d # ab,ac,bc,bd,cd
接続行列（有向グラフ）
B2 = [[ 1, 1, -1, 0, 0, 0], # a [-1, 0, 0, -1, 1, 0], # b [ 0, -1, 1, 1, 0, 1], # c [ 0, 0, 0, 0, -1, -1]] # d # ab, ac, ca, cb, bd, cd
隣接リスト（無向グラフ）
G1 = {"a": ["b","c"], "b": ["a","c","d"], "c": ["a","b","d"], "d": ["b","c"]}
隣接リスト（有向グラフ）
G2 = {"a": ["b","c"], "b": ["d"], "c": ["a","b","d"], "d": []}
グラフのアルゴリズム
- 最短経路問題
- 重み付きグラフ
- 集積コスト
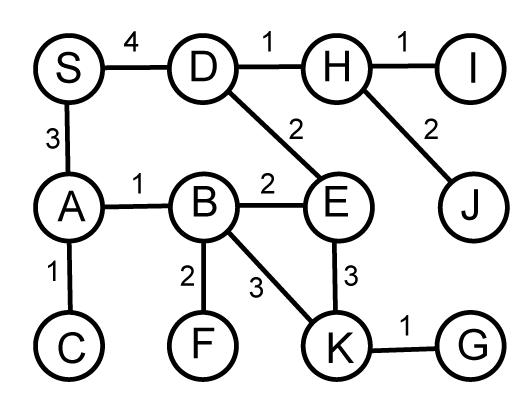
コストつき迷路グラフ
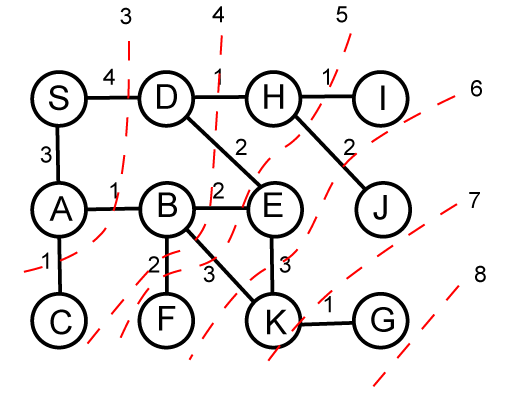
集積コストの等高線
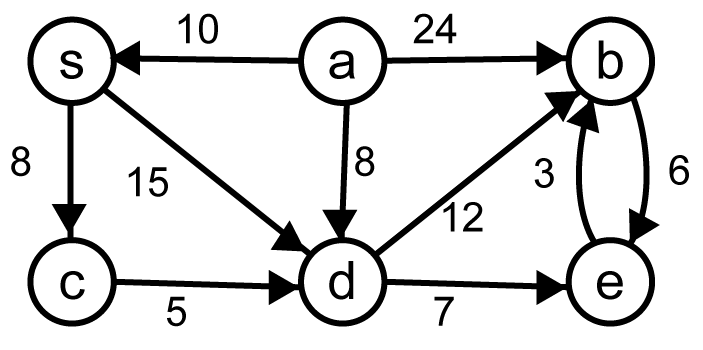
Dijkstra のアルゴリズム
- 有向グラフ
- 重み無限大 -> 999
- cost, parent 表
- アルゴリズム
- Python プログラム
- 最初のプログラムにバグがありました。１種類のテストデータで正しい結果が出ても、ほかのデータで計算すると間違いになることがあります。「先生のミスは生徒の経験」になるように、よく見比べてください。（# を使ってコメントアウトしたところがバグです。）
有向グラフ
問題
- 次の図（教科書p126）の迷路をグラフで表しなさい
