Views
Document
Event
File
Folder
Image
Link
News Item
Photo
Photo Album
Topic
Weblog
Wiki Page
木構造
Document Actions
算術式
- ( x + y ) / ( ( z - v ) * w ) )
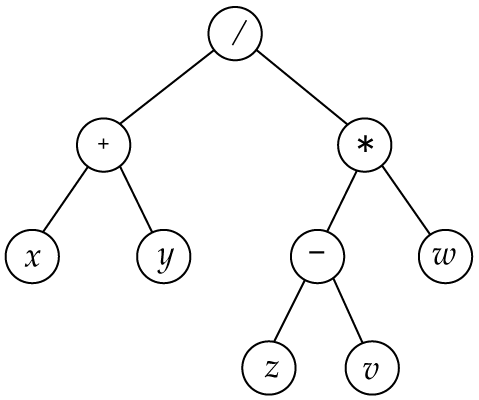
算術式の生成規則
- 算術式の木構造 -> △
- △ -> □ | △-○-△
- ○ -> + | - | * | /
- □ -> <変数> | <定数>
BNF (Backus-Naur Form)
- <式> ::= <数> | "(" <式> ")" | <式> <演算子> <式>
- <演算子> ::= "+" | "-" | "*" | "/"
- <数> ::= <変数> | <定数>
文法のあいまいさ
- x + y - z は
- ( x + y ) - z
- x + ( y - z )
- 掛け算・割り算の優先規則
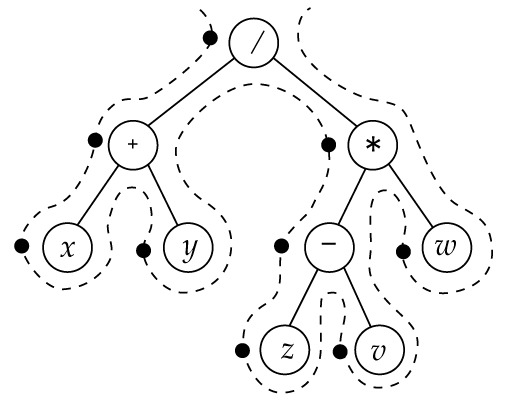
先順走査
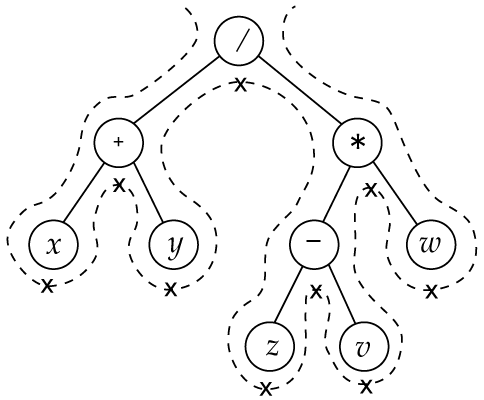
中順走査
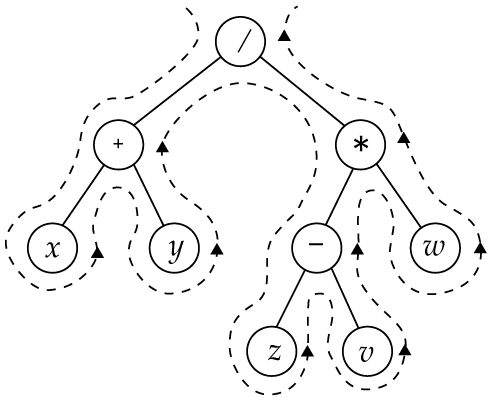
後順走査
演算の記法
- 前置記法： - A B
- minus(A, B) のような関数記法
- 中間記法： A - B
- 計算順序のあいまいさ -> 括弧が必要
- 後置記法： A B -
- A から B を 引く
- 逆ポーランド記法
スタックとポーランド記法
- ヒューレットパッカード社(HP) 電卓
- (3+21)/(9-6) -> 3 21 + 9 6 - /
- Python のリストを使った電卓
2分木
- 根(root) と呼ばれる節(node) を１つ持つ。
- 根及び互いに素な2分木 Tl, Tr からなる。
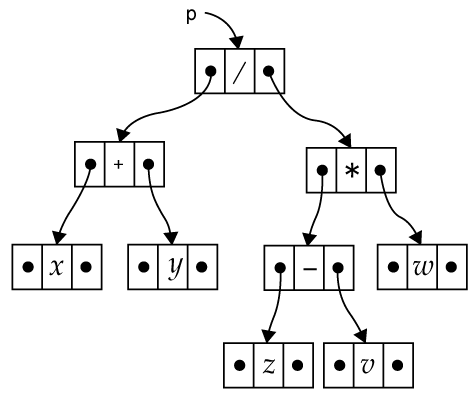
2分木の物理表現
Python のリストによる表現
[[[], "x", []], "+", [[], "y", []]], "/", ...]- 先順探索
def ltrav(p): print p[1], if p[0]: ltrav(p[0]) if p[2]: ltrav(p[2])
N分木(N進木)
- 根(root) と呼ばれる節(node) を１つ持つ。
- 根及び互いに素な N分木 T1, T2, ... Tn からなる。
枝分け (parse)
- 式の解析 (式 -> 木)
- 式 の BNF から 状態遷移図を作成
- 状態遷移図より解析プログラムを作成
BNF example
- <式> -> <数> <OP> <数>
- | <式> <OP> <数>
- 入力の最後 : $
状態図 example
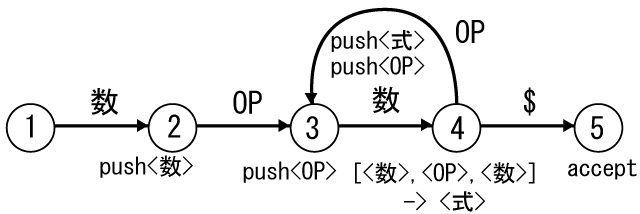
- プログラム
- 間違ってもこのプログラムを仕事に使わないように
実際の Compiler では
- 語句解析 (lexical analysus)
- 構文解析 (syntax analysis)
- ここで <式> を枝分け (parser)
- 意味解析 (semantic analysis)
- コード生成 (code generation)
Parser Generator
- 構文規則 (eg. BNF) から Parser を作る
- yacc (Yet Another Compiler Compiler)
- bison
- eqn.y
問題
- 逆ポーランド記法で書かれた次の計算をしなさい。また括弧を使った普通の記法に変えなさい。
- 100 100 + 5 / 20 2 / +
