Views
Document
Event
File
Folder
Image
Link
News Item
Photo
Photo Album
Topic
Weblog
Wiki Page
データ構造とアルゴリズムの基礎
Document Actions
積み木の塔を例題に、処理手順・データ構造・制約条件・アルゴリズムの概念を学ぶ。
教科書どおりなので、教科書をじっくり読んだほうが理解しやすいかもしれません。
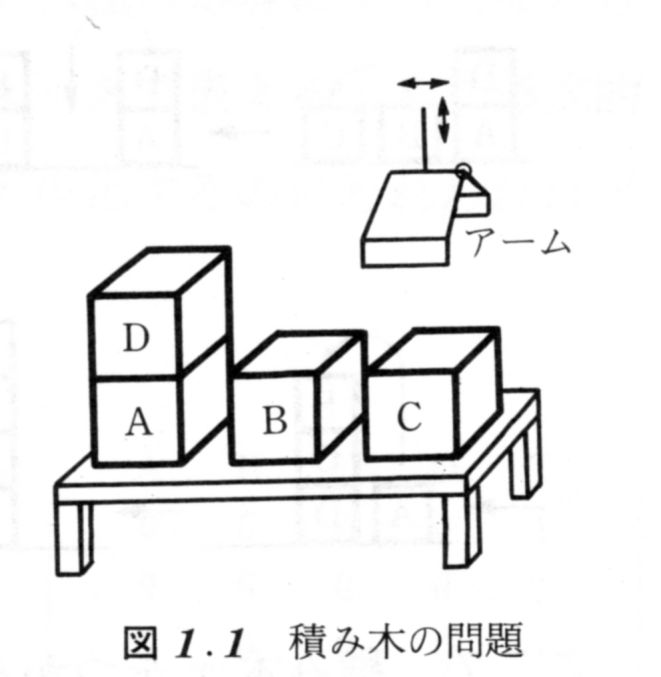
積み木の塔の問題
- テーブル面：積み木３個分
- 積み木：４個（Ａ，Ｂ，Ｃ，Ｄ）
- １本の積み木の塔を作る
- 上から順にＡ，Ｂ，Ｃ，Ｄ
図
計算機で解くには
- 問題を形式的モデルで表現する方法を決める（データ構造）
- そのモデルに対して解を見つける方法を決める（アルゴリズム）
頭で解く
手順を関数を用いて表現
move(x,y)... x の積み木を y の上に移動するremove(x)... x の積み木をテーブルの空いた場所に移動する
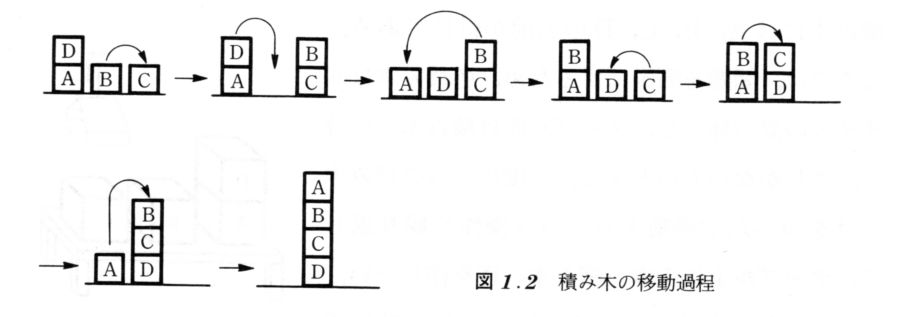
図1.2の手順
- move(B,C) -> remove(D) -> move(B,A) -> move(C,D) -> move(B,C) -> move(A,B)
別の手順
- move(C,B) -> remove(D) -> move(C,D) -> move(B,C) -> move(A,B)
モデル化（１）
- x が y の上に乗っている表
\ A B C D T A 0 0 0 0 1 B 0 0 0 0 1 C 0 0 0 0 1 D 1 0 0 0 0
モデル化（２）
- （１）の表は次の真なる事象の集合
- {on(A,T), on(B,T), on(C,T), on(D,A)}
- それぞれの積み木がどの積み木（またはテーブル）の上にあるかの表
A B C D ------------ T T T A
制約条件
- 一つの積み木のすぐ上には一つ
- テーブルに接して載せることができるのは最大３つ
- 自分の上には載せられない
- 同時に２箇所には載せられない
- 移動は一回にひとつずつ
- 上に何も載っていない積み木が移動可
- 上に何も載っていない積み木又はテーブルに移動可
補助のための表
- 制約条件のチェック
- テーブル又は積み木のすぐ上に載っている積み木の数
- support# 表
A B C D T --------------- 1 0 0 0 3
アルゴリズム
- move(x,y) を実行すると
- is-on(x) := y；
- 初期状態では、
- move(B,C) はできるが、
- move(A,B)はできない
アルゴリズム（続き）
- remove(x)
- is-on(x) := T;
- 初期状態では不可
- move(B,C) の次なら remove(D) が可
最初の数手
move(B,C) remove(B) move(B,D) remove(D) move(D,B) move(B,D) move(B,C) move(C,B) move(C,B) move(C,D) move(D,B) move(D,C)
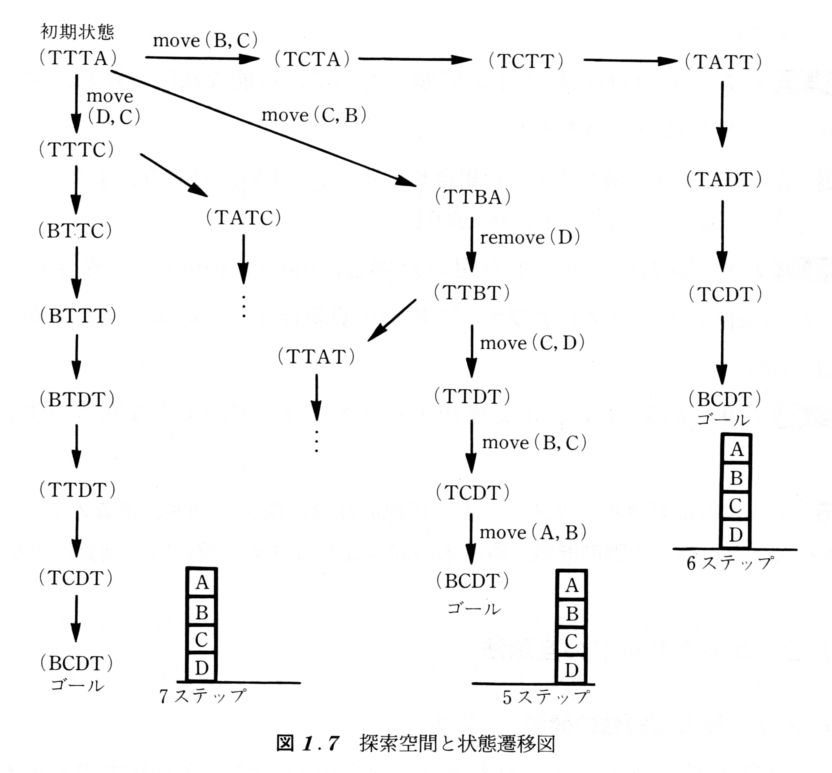
状態をリストで表現
- (T T T A) スタート
-> (T C T A) -> (T T T A) -> (T D T A) -> (T C T T) -> (T C T B)- -> (B C D T) 最終目標へ向かって探索
状態と状態遷移
- (T T T A) - move(B,C) -> (T C T A)
- 状態(state) ... 変数の取り得る値の組
- 状態遷移(transition) ... 動作、関数、...
探索空間と状態遷移図
例題１－７
- 可能な状態の総数はいくつあるか
- 制約条件を満たすような組み合わせを調べる。（？）
- 積み木置き場の区切りとして、, を使用
XXXX,, ... ABCDの順列 ... 24 XXX,X, ... 同上 ....... 24 XX,XX, ... 同上/2 .... 12 XX,X,X ... 同上/2 .... 12
- 答えが合わない。。。
本日の問題
- 制約条件 1 - 8 のうち、support#表でチェックできるのはどれとどれか。
解答
- (1) と (2) ... 数をかぞえる (1 or 3)
- チェックできないもの
- (3) 数しかないので、自分自身であるかどうかわからない
- (4) is-on 表に空白がないこと
- (5) is-on 表の１つの枠に2つ以上入っていないこと
- (6)から(8) move() 関数の制約
