画像フィルター

フーリエ変換

信号を波長の異なる波に分解する。

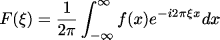
1次元のフーリエ変換
時間的に変化する信号(例:音、地震動、温度)を周波数毎の成分に分解する。 距離の関数として変化しているもの(例:水路にできた波)を空間波数成分に分解する。
2次元のフーリエ変換
距離と時間の関数として変化しているもの(例:水路にできた進行する波、電磁波、光) を空間波数と周波数の成分に分解する。 平面上の信号の強弱分布(例:画像)を空間波数成分に分解する。

フーリエ係数(フーリエ変換)の性質 ゆっくりした変化は ... 波数が小さい
小さいものは ... 波数空間での広がりが大きい

１次元のフーリエ変換

フーリエ逆変換

画像フィルター

フィルターとは、大きなものと小さなものをよりわけるフルイのこと である。大きなものは周波数でいうと小さな周波数を持ち、小さなもの は大きな周波数を持っているので、入力画像をフーリエ変換して、 適当な重み関数を掛けてやればよいことになる。

ところが、スペクトル空間での掛け算は実空間での畳み込み積分 (convolution)に相当するので、実空間のみでの計算が可能である。

ここで、g は畳み込み関数と呼ばれていて、G のフーリエ逆変換で 求める。

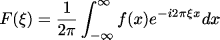
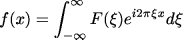
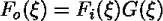
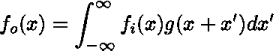
畳み込み積分は、走行平均(running average)を考えると理解しやすい であろう。走行平均はデータの平均を計算する窓をずらしながら平均値を 求めていくことでおおまかな傾向をつかもうとするものである。

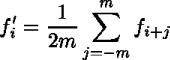
この計算を２次元のデータ構造を持つ画像データに適用する わけだが、この計算を行うツールとして、pnmconvolという コマンドがある。man pnmconvolを読むとわかる が、このコマンドの使用にはかなり注意が必要でである。

まず最初に、畳み込み関数の設計をする。この関数は PGM ファイル に作成する。 PGM ファイルのデータは正の整数値しかとれないので、 PGM ファイルフォーマットで定義される最大値の半分の値を 0 と解釈 するようになっている。また、最大値の半分で正規化されるので、平均計算 に必要な割り算はあらかじめデータに入っていなくてはならない。

以下の 3 x 3 の領域を平均化する例を見てみよう。

         P2
         3 3
         18
         10 10 10
         10 10 10
         10 10 10
この例では、最大値が18であるから、最大値の半分の 9 が 0 に相当する。 したがって、データ値 10 は、1 に相当する。また、正規化に使われる 数も 9 であるから、それぞれのデータ値は 1/9 の重みをもっていることに なる。もし、5x5 の平均をしたければ、最大値は 5x5x2 = 50、データ 値としては、25+1 の 26 を使えばよいことがわかる。

コマンドの実行は、低域通過フィルターの畳み込み関数ファイルを lpf.pgm としたとき、 

        % pnmconvol lpf.pgm johoto.pgm > joho-lpf.pgm
のようにする。 5x5 の単純走行平均をかけた例を以下の画像に示す。

上の例は低域通過フィルターであるが、元の画像から、低域通過フィルターを 通した画像を差し引けば高域通過フィルターができる。5x5の高域通過フィルターの 例は以下のとおり。(右の表はオフセットを除いた整数値) 
        P2
        5 5
        50
        24 24 24 24 24    -1 -1 -1 -1 -1
        24 24 24 24 24    -1 -1 -1 -1 -1
        24 24 49 24 24    -1 -1 24 -1 -1
        24 24 24 24 24    -1 -1 -1 -1 -1
        24 24 24 24 24    -1 -1 -1 -1 -1
この例では畳み込み積分の実行で負の計算結果は 0 に丸められてしまうことに 注意すること。以下の結果の画像は、結果を見やすくするために ガンマ値を 10 にして補正してある。

フィルターには今までのような上下左右に対称なものだけでなく、 非対称のものもある。例えば 
        P2
        3 3
        2
        1 2 1            0  1  0
        0 1 2           -1  0  1
        1 0 1            0 -1  0
のようなフィルターを使うと、これは右上から左下方向への微分を表す ことになる。このフィルターを適用した結果は以下のとおり。

このような非対称フィルターはエッジの検出に使われることがある。 よく使われるもののひとつに Sobel のオペレータと呼ばれるものがある。 x 方向、y方向のエッジの検出に、それぞれ以下のようなフィルターが 用いられる。 
          -1  0  1         -1 -2 -1
       X: -2  0  2      Y:  0  0  0
          -1  0  1          1  2  1
結果は以下のようになる。それぞれ x,y 方向の線をとらえている ことがわかる。

実際のエッジ検出には逆方向の微分も必要であり、pnmconvol だけを使って この計算を行うのは煩雑になる。pgmedge というコマンドは x y 方向の Sobel のオペレータを使ってその2乗和を出力している。 以下が実行例である。