画像の幾何学と幾何補正
センサの幾何特性
リモートセンシングの主なセンサタイプ
| 中心投影方式 |
狭義の中心投影方式
(フレームセンサ:フレームカメラ、テレビカメラ等) |
| ラインセンサ:リニアアレイセンサ,プッシュブルームスキャナ
(SPOT HRV, MOS-1 MESSR etc.) |
| ポイントセンサ:オプティカルメカニカルスキャナ
(Landsat MSS, NOAA AVHRR etc) |
| 非中心投影方式 |
Side Looking Radar, Side Scan Sonar, Synthetic Aparture Radar |
中心投影方式のセンサ
リモートセンシングではセンサの位置と観測対象(地表)との対応が時々刻々変化する。
このため、画像座標系を(u,v)、観測対象物空間の座標系を(x,y,z)で表す。
ある時刻tでのセンサの投影中心を(x0,y0,z0)、
センサの姿勢を(ω,φ,κ)で表す。但し、姿勢はz軸の正方向に対して左回りにκ
の角だけ回転し、次にy軸の正方向に対して左回りにφの角だけ、最後にx軸の正方向に
対して左回りにωの角だけ回転した状態にある。また、センサの投影中心から画像投影
面に下ろした垂線の足の位置を画像座標系で(u0,v0)とする。
このとき、以下の関係:共線条件式(colinearity equation)が成り立つ。
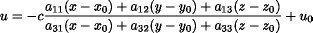
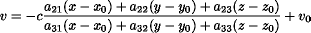
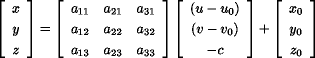
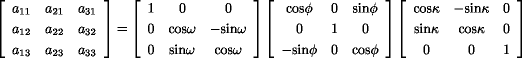
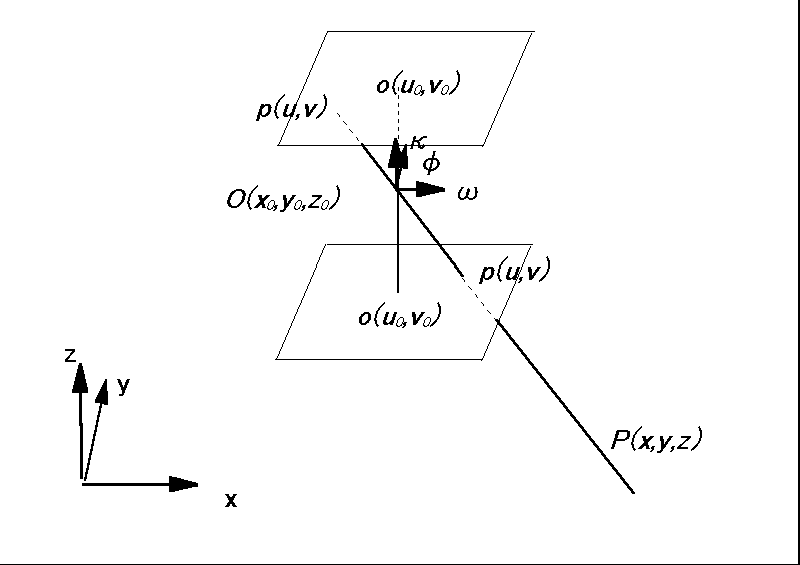
一般には、投影中心O(x0,y0,z0)、姿勢(ω,φ,κ) 主点の位置(u0,v0)は時刻tの関数である。
フレームセンサ(中心投影方式センサ
画像全体にわたって時刻によらず1点の投影中心を持つ。
ラインセンサ
走査線毎に投影中心が異なる。
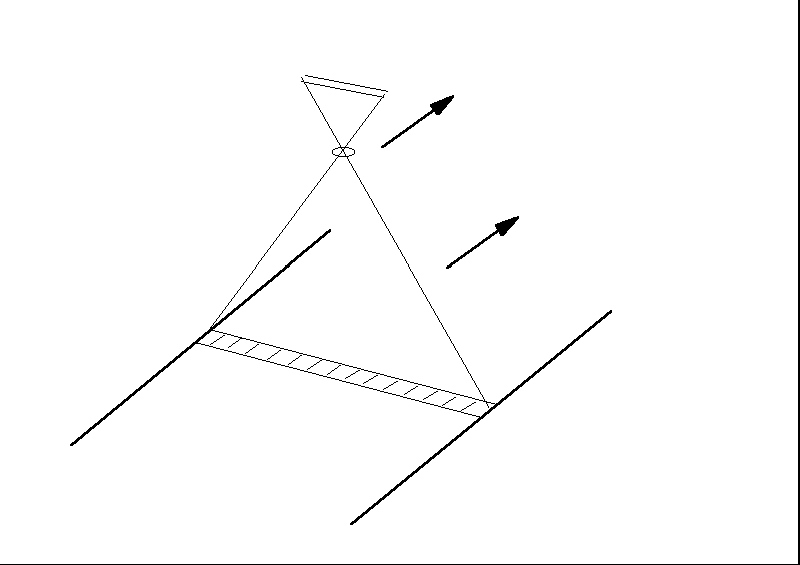
ポイントセンサ
画素毎に投影中心が異なる。
幾何ひずみ
レンズによるひずみ
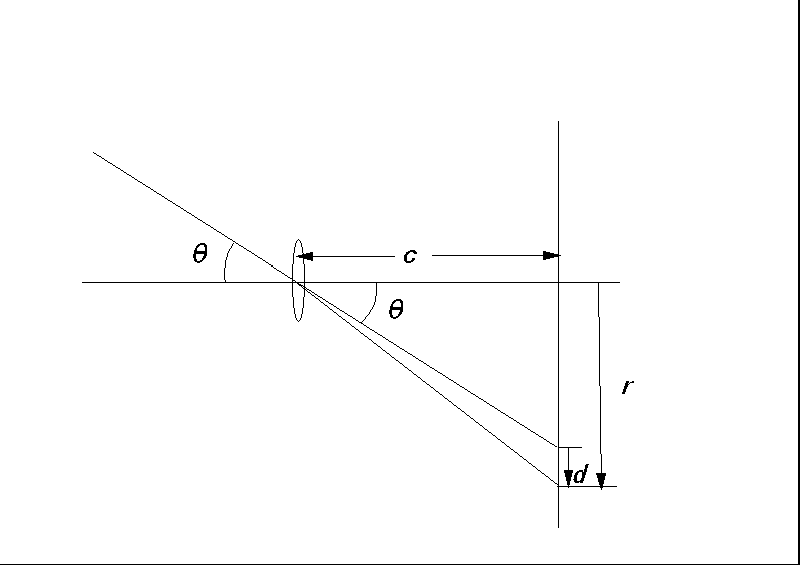 d = r - c tanθ
d = r - c tanθ
d = a1r + a3r3 + a5r5 + ...
この幾何学的歪み(放射状歪み)を作り出す
プログラム例
但し、画像のサイズによって係数が変わるので何にでも使えるというわけではない。
 ->
-> 
幾何補正
幾何補正の手順
- 補正式(座標変換式)の決定
- 理論的補正式による幾何補正(系統的補正)
センサの機構に関する内部歪みやセンサの位置や姿勢に関する
外部歪みを理論的補正式を用いて補正する。
人工衛星画像の場合、LANDSAT MSS で約1km(10画素)の誤差。
- 基準点を用いて決定する補正式による幾何補正(非系統的補正)
- 拡大・縮小
pbmplus のコマンド:pnmscale, pnmreduce, pnmenlarge
- 回転
pbmplus のコマンド:pnmrotate
- 反転
pbmplus のコマンド:pnmflip
- 平行移動
pbmplus のコマンド:pnmcrop, pnmmargin
- スキュー(シアー)
pbmplus のコマンド:pnmshear
- アフィン変換
u = ax + by + c
v = dx + ey + f
- 疑似アフィン変換(共一次変換)
u = a1xy + a2x + a3y + a4
v = b1xy + b2x + b3y + b4
- ヘルマート変換(一次等角変換)
u = ax + by + c
v = -bx + ay + d
縮尺 m = (a2 + b2)1/2
回転角 θ= tan-1(b/a)
- 二次等角変換
u = ax + by + c(x2 - y2) + 2dxy + e
v = -bx + ay - d(x2 - y2) + 2cxy + f
- 射影変換
u = (a1x + a2y + a3)/(a7x + a8y + 1)
v = (a4x + a5y + a6)/(a7x + a8y + 1)
- 3次元射影変換
座標変換式の係数決定には係数の数以上の基準点の座標を用いて
最小2乗法によって求める。
- 理論的補正式と基準点を用いて決定する補正式とを組合せた補正式による幾何補正
(併用補正)
- 理論補正により大きな幾何歪みを除去した後で基準点を用いた非系統補正をおこなう。
- 内部歪みや外部歪みに関するパラメータを基準点から決定する。
- 再配列(逆変換)
幾何補正後の出力画像の配列に対応するように、入力画像のデータを
並べなおす。入力画像の各画素について変換後の位置を計算する方法と、
出力画像の各画素について入力画像の座標系での位置を計算する方法とがある。
出力画像にすきまなく画像データを並べるために普通は後者の方法が用いられる。
- 内挿
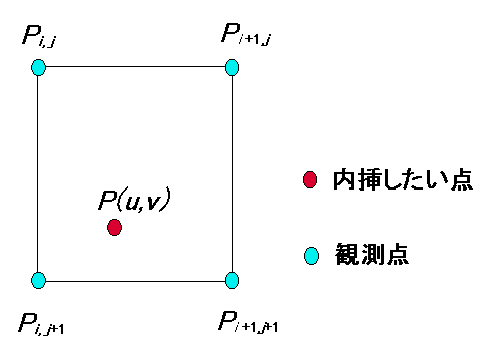
- 最近隣内挿法
P = Pi,j
i = [ u + 0.5 ]
j = [ v + 0.5 ]
- 共一次内挿法
| P = | {(i + 1) - u}{(j + 1) - v} Pi,j |
| + {(i + 1) - u}{v - j}Pi,j+1 |
| + {u -i}{(j + 1) - v}Pi+1,j |
| + {u -i}{v - j}Pi+1,j+1 |
i = [u]
j = [v]
- 3次畳み込み内挿法
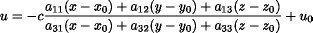
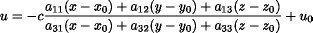
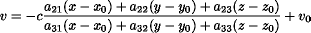
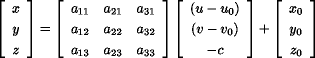
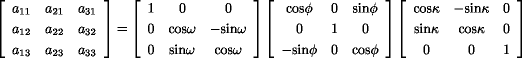


 d = r - c tanθ
d = r - c tanθ ->
-> 
