色彩理論
加法混色と減法混色
- 加法混色 ... 異なる色の光をスクリーン上に重ねて投影する。
... 加法三原色
- 減法混色 ... 白い光の前に異なる色のフィルターを重ねる。
... 減法三原色
加法混色による等色実験
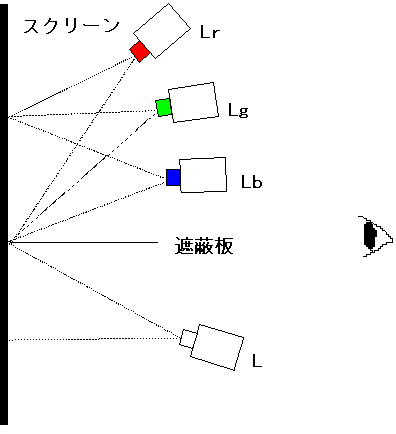
Lをテスト光として、上下の色が同じになるように上の3つの光源を調節する。
C = αR + βG + γB
3原色の光をどう調節してもテスト光の色と等色にならない場合がある。このとき
原色のどれかをテスト光に加えることで等色にすることができる。この場合 α, β, γの
どれかが負の値をとるということになる。
α, β, γの単位として、「白色光」と等色にしたときの値 (lr,lg,lb)をとる。
C = RR + GG + BB
色空間と色度座標
色空間 ... R,G,Bを直交する3軸として、(R,G,B)を座標とするような色光の3次元表示ができる。
色度座標 ... 色空間で (1,0,0), (0,1,0), (0,0,1) を頂点とする正三角形と、ベクトル(R,G,B)
との交点を (r,g,b) で表す。
r + g + b = 1
色三角形はこの正三角形上に色立方体の側面を投影したもの。
(r,g,b) のうち独立は2つだけなので、(r,g) で表す ... rg 色度図
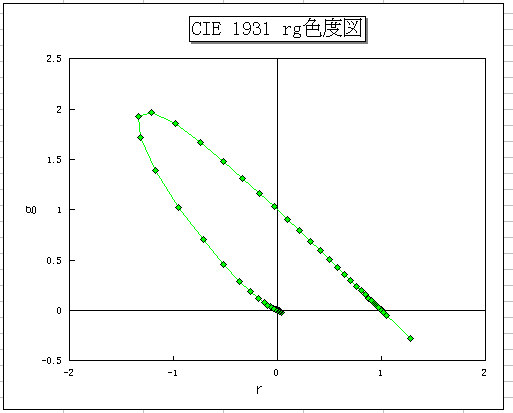
CIE (Commision Internationale de l'Eclairage, 1931) RGB 表色系
- 3原色を 700.0, 546.1, 435.8 nm の単色光とする。
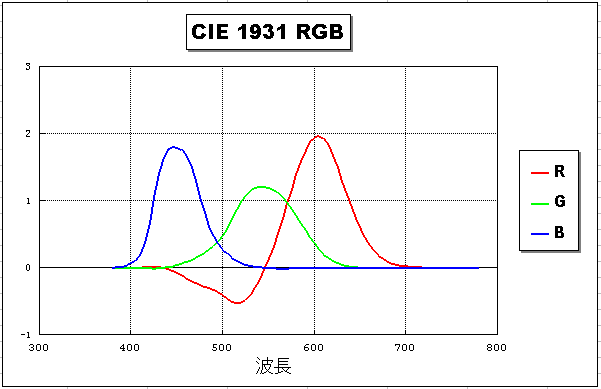
- 明度係数 (lr:lg:lb) = (1:4.5907:0.0601)
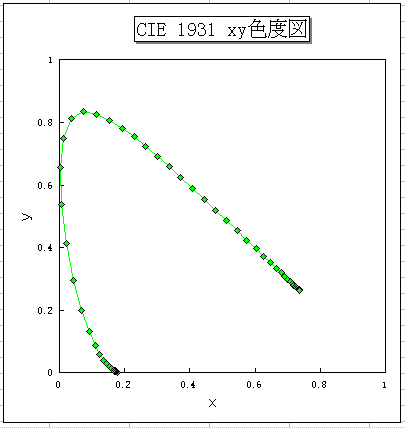
- 単色光を rg 色度図にマッピング
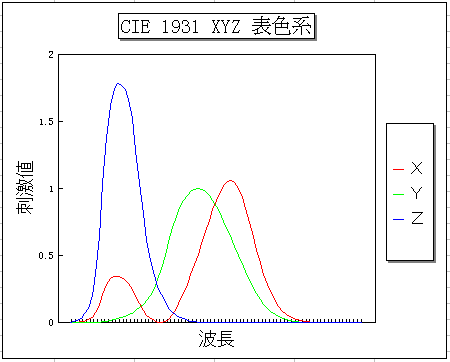
CIE XYZ 表色系
| X = | 0.49000 R | +0.31000 G | +0.20000 B |
| Y = | 0.17697 R | +0.81240 G | +0.01063 B |
| Z = | | 0.01000 G | +0.99000 B |
CIE 1976 UCS 色度図
Uniform Chromaticity Scale diagram
xy 色度図上の色度点間の距離を、感覚的な色の性質の差に比例するように改良したもの。
(見分けることのできる最小の色度差を実験によってもとめる)
| u' = | 4x / (-2x+12y+3) | = | 4X / (X+15Y+3Z) |
| v' = | 9y / (-2x+12y+3) | = | 9Y / (X+15Y+3Z) |
実際の色を u'v' 色度図にマッピング
CMY 表色系
Cyan, Mazenta, Yellow
C = 1 - R, M = 1 - G, Y = 1 - B
YIQ 表色系
YCbCrともいう。
| Y = | 0.299 R | +0.587 G | +0.114 B |
| I = | 0.596 R | -0.274 G | -0.322 B |
| Q = | 0.211 R | -0.522 G | +0.311 B |
マンセル表色系
色を、「心理量を基準として」定義。
A. H. Munsellが提唱。
The Munsell System of Color Notation
色相(H)
Red, Yellow, Green, Blue, Purple の5色を基本色相とし、円周上に配置(色相環)
1-10R,1-10YR,1-10Y,..1-10RP の順に配置される。
明度(V)
Black(0) ... White(10)
彩度(C)
色のあざやかさ。無彩色(/0) から最もあざやかな「単色」まで。/4 /8 のように表す。
最大値は色相明度により異なる。
マンセル立方体
ある色は 例えば 5R4/14 (色相 5R 明度 4 彩度 14) のように表す。色相を円周に配置し
明度を高さに、彩度を中心からの距離で表すことでマンセルの色立方体ができる。
HSV 変換
マンセル色立方体に類似の色円柱を RGB から導いて利用する。
R,G,B は 0から1に、Vは0から3、Hは0から2π、Sは0から2/3に規格化されている。
H = tan-1{(G-B)/(2R-G-B)}
S = {(B-R)2+(R-G)2+(G-B)2}/3
V = (R + G + B)
逆変換は
R = V/3 + 2S cos(H/6)
G = V/3 - S cos(H/6) + S sin(H/2)
B = V/3 - S cos(H/6) - S sin(H/2)
(この他にも HSV については色々なモデルがある。詳しくは
「画像解析ハンドブック」(東京大学出版)の機能編第I部
2. 変換 2.1.2.3 HSI変換および逆変換を見よ。
上記の式は Raines の定義による (2.1.38,39))